Workshop Wednesday: 100-Grids and Flashcard Bingo

A 100-grid is another marvelous teaching and learning tool that can be made in numerous fun ways. A standard 100-grid contains the numbers from 1 to 100 (too obvious?) in ten rows of ten squares each, 1-10 in the top row, then 11-20 in the second row, and so on.

Draw the grid on the driveway with chalk; your kids may also get Dad’s permission to draw it on the garage floor if they promise to sweep it clean again when they’re done. I drew a 100-grid on an old tablecloth (you can also use an old bedsheet) with permanent markers for a reusable, storable, portable, floor-cloth version. These grids are big enough for your kinesthetic learners to hop around on for hopscotch-style, action learning!

Draw a smaller 100-grid on paper or cover the blank-grid side of a Scrabble Junior game board with clear Con-Tact paper (to make it washable & more durable) and fill in the numbers with either wet-erase or dry-erase markers. These versions are more tactile, since your students can use game pawns, pennies, or dry beans for marking number squares in learning activities.

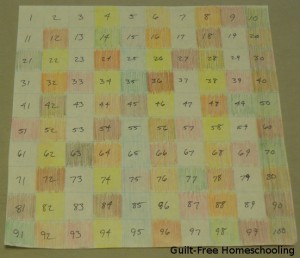
Add a visual learning element to your 100-grid activities by alternating colors of the numbers. To skip-count by 2’s, write the odd numbers in one color and the even numbers in another color. To skip-count by 3’s, use one color for the multiples of 3 and another color for all the other numbers. If you want to do this activity many times for many multiples, write all the numbers out in one color, then place a colored marker on the appropriate skip-counting intervals.

Do you have an auditory learner? Challenge him to say the numbers aloud while hopping or jumping from number to number, or while placing markers on the correct squares.

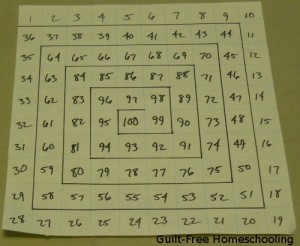
Try varying the arrangement of the numbers in your grid for some interesting game play. If you have a Chutes and Ladders game, you can see one simple variation of our grid — it starts in the lower left corner and zig-zags back and forth to the top. For another game board variation, start with 1 at an outer corner and spiral the numbers in toward the central 100 square–but you might want to outline the path to make it easier to follow.

For a very simple game to practice math skills using these novelty grids, remove the face cards from a normal deck of playing cards and use the remaining “math deck” for an addition game. Let each player select a pawn and set it just off the grid near the 1 square; on his turn, each player will turn up a card from the deck and move his pawn that many spaces. The first player to reach 100 wins that round. For more advanced play, let the black cards represent positive numbers (adding, or moving forward) and let the red cards represent negative numbers (subtracting, or moving backward).

Another amazing math activity is the “Sieve of Eratosthenes.” This scholar from long, long ago created a fairly simple mathematical process for isolating prime numbers. On a standard 100-grid, have your students cover each multiple of 2, starting after 2 itself, to cover each number that has 2 as one of its factors. Since 2 has only itself and 1 as factors, leave it uncovered; it is a prime number. Now repeat with 3, covering each number after 3 that is a multiple of 3. Continue for 4, 5, 6, 7, 8, and 9. The numbers that are left uncovered are all prime numbers that have no other factors besides themselves and 1. This is fun to do on paper, using colored pencils to color in the squares and using a different color for each round. Starting with a light color and getting a bit darker on each round will show very plainly which numbers have the most factors — they will be very dark when you have finished.

Now for a bonus — here are the instructions for a game I call “Flashcard Bingo,” that is played on a 100-grid.

FLASHCARD BINGO

Equipment:

• 1-100 chart
• Math flashcards–combine addition, subtraction, multiplication, and division flashcards (The combination of cards used should be appropriate to the players’ skills.)
• Several dozen markers for each player (colored paper squares, pennies, dry beans, etc.). If playing outdoors, larger objects, such as poker chips, can be used as markers.

Shuffle all the flashcards together and place them in an index card file box or other box that will hold all the cards and allow extra room for fingers to draw them out.

Use the honor system for not peeking at the answers if they are printed on the cards, or have players draw & hold cards for each other, covering answers as needed.

The first player draws a card at random and gives the answer to the problem. If he gives the correct answer, the player puts his marker on the answer number’s square on the 100-grid. If the card has two different problems on front & back, he may look at both problems and choose either side of the card for strategy: if the player already has possession of the square for that card’s answer, he may choose to answer the problem on the opposite side.

If the player gives an incorrect answer, the next player gets a chance to answer correctly and “steal” the square. If the second player cannot answer correctly, each player in turn is given a chance to answer and steal the square with the correct answer. The player giving the correct answer may not be holding the flashcard or may not have seen the answer on the flashcard.

At the end of a player’s turn, his card is returned to a random location in the box. Play proceeds to the left of the player who drew that card, even if he answered incorrectly, and even if the player who gave the correct answer is the next player in the circle.

If a player’s answer number is already covered by another player’s marker, the new player may “bump” the occupying player’s marker off the grid and place his own marker on the square, or the player may opt to take another card instead of bumping the occupying player’s marker.

If the player already has possession of the squares for both sides of the card, he may announce that he will combine both answers as desired (adding, subtracting, multiplying, or dividing) to achieve a hard-to-reach number square, such as prime numbers or large numbers. Paper & pencil may be permitted, but not calculators. If a player draws a flashcard with a correct answer of 0 or an answer larger than 100, and he is not able to combine the answers from both sides of the card, he may opt to draw again. There is no limit to how many cards a player can draw, as long as he already owns the squares representing the answers to the cards drawn, but he must use the first available square.

Winner is the first player to get 5 markers in a straight row, vertically, horizontally, or diagonally.

Advanced Option: Add a game die for another challenge. Players roll the die on each turn and add, subtract, multiply, or divide that number into the answer on the flashcard to determine which square to occupy on the grid.

Discussion Question: As your students play this game, ask them if they notice which part of the grid accumulates the most markers and if they can explain why that happens.

Younger Players Option—

Use only addition & subtraction facts from 1-20. Play on a 20-grid with 4 rows of 5 squares each (1-5, 6-10, 11-15, 16-20). Winner is the first player to get 4 markers in a straight row in any direction, vertically, horizontally, or diagonally.

For more ideas, see also:
Applying Learning Styles with Skip-Counting
Hopscotch–A Powerful Learning Game