Homeschool How-To's - Guilt-Free Homeschooling

Workshop Wednesday: Freebie Magnets

June 13, 2012 by CarolynM 2 Comments

Magnets are a wonderful learning tool for tactile learners. There is something about that magical, magnetic connection that appeals to fingers of all ages. Fortunately, most of us have a ready supply of free advertising magnets from the pizza place, the hairdresser, the auto mechanic, the new phone directory, and every politician who marches in a summer parade. Peel your collection off the refrigerator, and let’s turn them into some great learning aids. I’ll list several possible uses and some basic how-to’s for the magnets. You’ll want to analyze what topic your students are struggling with or where they need the most help, and then focus your efforts there. Students can also help make magnetic learning aids, and helping to make them means the learning begins right away.

Stickers are probably the easiest things to turn into magnets, since you just have to stick them onto a magnet and cut around the stickers with scissors or a razor knife (such as an X-Acto). I have used scrapbooking stickers that looked like Scrabble letter tiles, foam letter stickers that were shaped like small jigsaw puzzle pieces, and 3-dimensional plastic stickers with raised animal shapes. The puzzle piece stickers were slightly tricky because of their irregular shapes, but I cut the magnets into squares small enough to fit in the center of each sticker, and then (after attaching the magnets) dusted the surrounding sticky edges with baby powder, using a dry artist’s paintbrush. It took two rounds of dusting powder to get the foam pieces to stop sticking to each other, but I’ve had no problems with them since then. With regularly shaped stickers, it is fairly simple to line them up next to each other (as many as will fit on the magnet), press them down securely, and then cut them apart. If your stickers have rounded corners, cut them apart as squares first, then round off each corner with scissors. There may be a strip of magnet left at the side that is too narrow to hold more stickers, but hang onto that piece—you’ll cut it up and use it later.

Once upon a time, my kids had some puffy stickers that they wanted to be able to save and reuse. Magnets to the rescue! I covered the backs of the stickers with adhesive plastic, then attached a magnet to each one. Those cartoon character magnets became a great quiet toy for imaginative play.

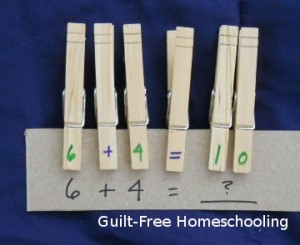
Craft foam sheets allow you to make your choice of subject matter by writing on the foam with a permanent marker, such as a Sharpie. (Some foam sheets can even be purchased with a magnetic backing already attached!) I had some magnetic strips that were adhesive on one side (leftovers from a weather-stripping project), so I cut squares of craft foam the same width as the magnetic strip, stuck them on, and cut the magnetic strip between the squares. Adding numbers to each square produced magnetic manipulatives for math! I drew arithmetic operation symbols on a few more squares to complete the set.

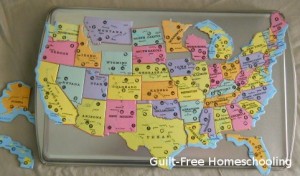
Laminated placemats have been featured in a previous Workshop Wednesday article, but I will mention them again here for good measure. That example showed a periodic table of elements placemat that I turned into magnets, but any subject matter will do. If a placemat doesn’t lend itself to a building block format (such as the periodic table) or a map (USA, etc.), perhaps you can cut it into a simple jigsaw-style puzzle to entice your kids to play with the magnetic pieces and learn the information.

I have also used the plain (back) side of a thick foam-like vinyl placemat by cutting it into the desired shapes and attaching a small piece of leftover magnet to the back of each piece (formerly the front of the placemat). Adhesive squares made for scrapbooking, card making, and other popular paper crafts work great for attaching magnets (without the mess and hazards of hot glue guns). These vinyl-foam placemats are a bit heavier than craft foam and are made of a material that is not subject to the static electricity that can leave you covered in bits of craft foam for the rest of the day. Yes, that is a magnetic map of Iowa’s 99 counties, made from the backside of an orange jack-o-lantern placemat, but please don’t feel you have to try something quite so ambitious as your first project (that thing was tricky!).

A USA jigsaw puzzle (cut on state borders) received new life as a magnetic puzzle with the addition of a magnet square to the back of each puzzle piece.

Letter game tiles were repurposed with the addition of a magnet on the back of each tile.

Sandpaper cut into small squares can be glued to cardstock for added strength and then attached to a magnet. Grab your Sharpie marker again and write or draw letters, numbers, symbols, etc. for magnetic manipulatives with a bonus tactile texture. I made some in 1” squares, but don’t let that limit your imagination!

Funny facial features (eyes, eyebrows, noses, mouths, mustaches, ears, etc.) drawn on cardstock and attached to magnets become a fun game for preschoolers (I saw that idea on Pinterest, but I don’t know who originated it; someone deserves the credit!). Now what if you used the same principle for body parts and made interchangeable heads, bodies, legs, feet, arms, and tails for a magnetic build-a-monster activity? Build-a-bug, build-a-robot, build-a-car, build-an-animal, build-an-alien—the possibilities are endless! Your older students may have fun creating these magnets for their younger siblings, and they’ll learn some great problem-solving skills in the process. I wonder if we can make these small enough to fit in this empty Altoids tin? Hmmm… then Mom could keep it in her purse for Timmy to play with in church or while waiting in a restaurant!

So let’s review: we’ve discussed making magnets for letters to use for phonics and spelling practice, numbers and operation symbols for math, chemical elements for science, and states for geography. Need more ideas? How about geometric shapes, colors, incrementally-scaled pieces for number value (make them match the size of other math blocks you may own), fraction pieces, or pattern blocks. Have a struggling reader? Use the “magnetic poetry” type of word magnets (purchased or home-made) to focus on reading one word at a time, then adding them together to build a sentence. Have a struggling writer? Those same magnetic words can help him write sentences, stories, or poetry, since it can be much easier to rearrange someone else’s words than it is to think up new words from your own head. Pick up a small, inexpensive, cardboard skeleton party decoration, cut it apart into individual bones or groups of bones (such as the rib cage, hands, feet, etc.), attach some magnets, and you have an anatomy learning aid. Plastic or cardboard coins can become magnetic money manipulatives (say that three times really quickly).

When you have accumulated a large supply of educational magnets, the traffic in front of your refrigerator may get overly congested. Solution: steel cookie sheets or steel pizza pans are lap-sized and much more portable than the refrigerator door. If you need to shop for steel pans, you may want to take along a small magnet in your pocket for testing purposes. (That nosy store clerk will leave you alone when you explain that you’re obviously shopping in the kitchen section for educational materials.)

Now before I forget, there is one other accessory that makes magnetic learning aids even more beneficial: paper. I drew a Sudoku grid large enough to hold our number magnets and placed it on the cookie sheet, using the magnets to hold it in place. Ta-da, magnetic Sudoku can take the visual puzzles from a book or newspaper and turn them into a tactile masterpiece. A worksheet with fill-in-the-blank problems could hold magnets on those blanks instead of written answers. Your kids might choose to color an underwater background picture to place behind their letter magnets, just because they are learning to spell the names of ocean creatures.

Learning isn’t limited to books, life doesn’t happen between the pages of a workbook, and we learn what we enjoy. Magnets get fingers involved, and fingers love to learn! So what are you waiting for???

Filed Under: Activity Ideas, Homeschool How-To's, Learning Outside the Books, Learning Styles, Math, Phonics, Preschoolers, Reading, Roadblocks to Learning, Science, Spelling, Tactile Learning, Workshop Wednesday, Writing

Workshop Wednesday: Clothespins

June 6, 2012 by CarolynM Leave a Comment

Clothespins? Yes, ordinary spring-type clothespins can be turned into some pretty snazzy manipulatives and still be pressed into laundry duty as needed. I used a Sharpie permanent marker to write on the “business end” of each clothespin. See the entire alphabet? (click on photos to enlarge)

I made my clothespins with upper case letters. Your students can practice matching them up with their lower case “little brothers” on flashcards, even homemade ones like this piece of cereal box cardboard.

Did you notice that the first pic had the clothespins facing one way and the next pic had the clothespins facing the other way? Good for you—you’re very observant! I wrote the letters on both sides of the clothespins, carefully facing them in opposite directions, so that the pins could be used either up or down. Here’s one pin I took apart, so you can see both sides at once.

I repeated this trick with numbers and arithmetic operation symbols. These are clipped onto a wire hanger to spark your imagination with more ideas for use!

And here’s a quick math problem with clothespins:

You can make multiple sets of letters and numbers with these low-cost, multi-purpose manipulatives. Let your early learners sort the letters in alphabetical order or clip the clothespin letters onto matching flashcards, letter tiles, or the title words on their favorite storybooks. Use the pins for phonics practice, challenge your students to form their spelling words, or leave silly messages on the clothesline. Bring a different tactile dimension to math lessons by letting the littles sort the numbers in order, combine pins for multiple-digit numbers, or include the operation symbols for writing out math problems. Best of all, these manipulatives can do double duty on laundry day, and your students will get plenty of stealth learning practice when they sort the pins out again for lessons!

For more fun, combine these with:
ABC Flashcards
What Is the Missing Element?
Letter & Number Recognition

Filed Under: Activity Ideas, Homeschool How-To's, Kinesthetic Learning, Math, Phonics, Preschoolers, Tactile Learning, Workshop Wednesday

Workshop Wednesday: Building Blocks for Success in Spelling

May 30, 2012 by CarolynM Leave a Comment

Spelling, like math, is a subject that requires several foundational skills learned in sequential order, as shown in the diagram, beginning at the bottom and building up, one skill upon another. No one is born knowing how to spell correctly, but the individual steps to spelling proficiency can be somewhat tricky to identify by those who have already been reading for many years.

Skill #1 is the first building block: learning to recognize letters both by their names and by the sounds they represent. Since vowels can represent multiple sounds, depending on their combination with other letters, it is simplest to use their names and the short vowel sounds during the recognition phase. I preferred to teach my children upper case letters first, since that provides fewer opportunities for reversals (such as confusing b and d). Once the child knows the upper case alphabet well, the lower case letters can be introduced as the “little brothers” of the first set. Pairing the big brothers and little brothers together also helps avoid reversals, even when they don’t look that much alike—because kids easily understand the concept of siblings who belong together but aren’t identical.

Skill #2 is vital: correct pronunciation of each letter sound, leading to correct pronunciation of words as reading begins. A child must hear and speak the sounds correctly to be able to match those sounds to the appropriate letters. Some children may have already formed bad habits of mispronouncing certain sounds as toddlers (for example: difficulty with l’s, r’s, or w’s, lisping with a th-sound instead of an s, or dropping the initial s from sc-, sl- or sw-blends), but the visual application of learning the letters that represent those sounds can help straighten out the mistakes. However, if family members mimic the youngster’s incorrect pronunciation habits on a routine basis, confusion will follow, since the child who is learning to read won’t know which sound is correct! Take the time to instruct the child slowly and thoroughly so that he can learn to make the sounds properly. It is much better to learn correct methods in the loving security of home and family than to continue incorrect, juvenile habits into adulthood. Elmer Fudd’s manner of speaking may have been funny in cartoons, but if Elmer had been an actual person, his speech may have caused him to be taken less seriously in real life. Some local dialects can also twist the pronunciations of words away from their actual spellings, which is why television news reporters are encouraged to minimize regional forms of speech and learn to speak without a local accent.

Skill #3 consists of learning common patterns of letter combinations and the sounds made those combinations, known collectively as phonics. This level includes many different phonics patterns, from long and short vowels to vowel blends, consonant blends, and digraphs (the new sounds created by certain combinations, such as ch, ph, sh, th, and wh). Silent letters add another twist, but those are usually predictable, since they occur within specific combinations. (The ABC’s and All Their Tricks is a wonderful reference book, explaining the origins of spelling patterns, giving examples of words using each pattern, and answering the spelling questions that had stumped my teachers throughout my education.)

Skill #4 comes after the phonics patterns are mastered: syllable division is the next logical skill to achieve. Knowing how words separate into predictable syllables helps the student tackle new, longer words and get the pronunciation correct, usually on the first try.

The #5 building block skill for spelling success is learning prefixes and suffixes and being able to recognize them from the root word. We kept our large dictionary handy that showed the meanings of the individual components of each word—a fascinating study. My students loved compiling lists of words that were all based on a common root and seeing how the prefixes related to the words’ definitions—instruct, destruct, construct, etc. We played the Rummy Roots card games to learn common Greek and Latin roots that have become part of our everyday vocabulary. The mastery of roots, prefixes, suffixes, and other syllables was proven by accurately reading the list of chemical ingredients on a shampoo bottle!

As my children conquered each of these skills, I encouraged them to “hear the sounds in order” in each spoken word, so they could then write those sounds in the correct order for accurate spelling. It takes careful listening to spell words correctly, and the visual skills attained through these building blocks will work together with the sounds heard to achieve success.

Filed Under: Auditory Learning, Homeschool How-To's, Learning Styles, Reading, Roadblocks to Learning, Speech, Spelling, Visual Learning, Workshop Wednesday

Workshop Wednesday: Hopscotch – A Powerful Learning Game

May 23, 2012 by CarolynM 6 Comments

Who knew that a patch of concrete, some chalk, and a couple of rocks could produce a fun way to learn just about anything? When I was a little girl, I played hopscotch in the traditional way, tossing my stone and jumping from square to square, just as a game for practicing my tossing and balancing skills. Hopscotch can also be used as a kinesthetic learning method, involving the big muscles of arms and legs, pumping information through the blood vessels to the brain. I can see many other uses for the basic method of hopscotch, providing a great method for teaching preschoolers, kinesthetic learners, active children, or anyone else who just needs a break from sitting at a table for one more worksheet.

Let’s start by changing the standard hopscotch pattern to a row of 10 squares, numbered from left to right, and let your little ones practice counting as they hop from box to box and back again—tossing a marker stone or beanbag can be used later as their counting skills increase. Do the same thing with a row of ABC’s, first for letter recognition and later for reciting the sounds made by each letter or for a word beginning with that letter. Mom can say a word, and the child can hop to the letter that begins the word. For more advanced students, change the ABC’s to a grid pattern, and try “Twister Spelling” by putting hands and feet in the correct squares to spell the word. Use multiple beanbags, poker chips, or plastic yogurt lids for markers, and challenge your kiddies to spell out words by placing their markers on the correct letter squares.

You can also practice addition and subtraction facts with a hopscotch grid. Draw a 1-10 grid by making two rows of five squares each: 1-5, 6-10. Make these boxes large enough for your student to stand in, sort of like a hopscotch game. Start with simple addition problems by asking: If you put down [this many] markers, starting with Box #1 and putting one marker in each box, and then you add [this many] more markers, how many boxes will have markers in them? What is the largest number box that contains a marker? Repeat this activity with as many different number combinations as possible, until your student knows addition facts from 1-10 so well that he cannot be stumped. Then draw two more rows of boxes, extending the grid to 20 (11-15, 16-20), and continue the addition practice with problems up to 20. You can also work on learning doubles in the teens: 5+5=10, 6+6=12, 7+7=14, 8+8=16, 9+9=18, 10+10=20. These facts will help him with problems where the answer is between 10 and 20.

Does one of your students have trouble with subtraction? Using the 1-20 grid, pick a problem that may have stumped your child, like 13-9=? In this example, cover all numbers larger than 13. Ask: If you put down 9 poker chips, with one on each box, starting with 13 and counting down, what is the largest number box that will still be showing? If he’s already experienced at using the 1-20 grid of numbered boxes, he will be able to recognize the row of 6-10 as being 5 boxes. Then he can see that there are 3 boxes for 11-13, so those two rows will use 8 of his 9 poker chips; now he can put the last chip in the largest numbered box in the top row (the 5), and he’s left with 4 as the largest number box still showing: 13-9=4

Another helpful trick is to show your student how to work up or down from 10 when the answer to a problem doesn’t come to him immediately. For example, 13-9=? Let’s see, I know that 10-9=1, and 13 is 3 more than 10, and 3+1=4, so 13-9=4! How about 17-9=? 10-9=1; 17=10+7, and 1+7=8, so 18-9=8! Did you follow that? Children can get discouraged when they don’t know or can’t remember an answer immediately. Showing them several different methods for figuring out the answer helps them to see that they are smart enough to find the answer anyway. Working toward the answer from 10 or from the nearest double is a legitimate method of solving the problem and is actually a better way to learn than just rote memorization, since it uses more creative solving methods.

Are you ready to take this up one more notch? Help your students draw a 1-100 grid (10 rows of 10 squares each, numbered 1-100) and challenge your young mathematicians to toss two beanbags onto the grid and add the resulting numbers. Add more beanbags as their skills increase, or switch to subtraction or multiplication. Use beanbags in different colors (or marked with mathematical operation symbols) for students with appropriate abilities: Color #1 means add this number, Color #2 means subtract this number, Color #3 means multiply by this number, and Color #4 means divide by this number. Use several beanbags for each mathematical operation, drawing them at random from a bucket to create an amazing running math problem. Number squares can be chosen by random tossing or through careful aim. Challenging siblings to toss the beanbags and create problems for each other to solve may result in some serious stretching of math skills! Other possibilities are to toss two beanbags to create a fraction, then simplify it as needed—and more beanbags mean more fractions, which can then be added, subtracted, multiplied, or divided, always reducing the answer to its simplest form. The hopping part of hopscotch doesn’t come into play with this method (unless your kids figure out their own creative way to use it), but the tossing and retrieving of beanbags will still give your wiggly kids plenty of action.

Now you think you’ve heard all of the possible ways to use hopscotch in learning, right? Not at all! Let’s go back to the original hopscotch pattern, but instead of numbering the squares, write in parts of speech: noun, pronoun, verb, adjective, adverb, conjunction, preposition, prepositional phrase, and interjection. Hopping through the boxes gives the student a chance to think of a correct example word to give when he stops to pick up his marker. Use more specific terms as your students’ grammar skills increase: irregular verb forms, verb tenses, plurals, reflexive pronouns, dependent clauses, and so on. I included a “sentence” space at the end, and students should make their example sentences match the level of grammar being studied.

If you have a student who is really interested in science, specifically chemistry, and if you have access to a large patch of concrete, consider helping him draw out the periodic table of elements and numbering the squares accordingly. Let him make simple flashcards for each element to fit the boxes on his diagram (cereal boxes are a great source for inexpensive flashcards; write on the back with permanent marker) and practice putting them in their proper places. Flashcards might include the atomic number, the element name and symbol, and the atomic weight. More advanced students may want to include more detailed information and use the jumbo flashcards for memory practice. Other hopscotch applications: a diagram of the solar system would provide practice at naming the planets, a simplified skeleton could be drawn for practice at naming the bones, or a map of the United States (or any geographic area) would provide practice at naming states, capital cities, or other geographic features. Coordinate planes with x- and y-axes provide a large grid for plotting specific points with poker chips. Students of advanced math can solve complex equations, plot the points from multiple solutions, and draw the curves with yarn or string.

Any of these hopscotch learning games may also be drawn with permanent markers on an old, discarded sheet or tablecloth (check local thrift stores), resulting in a reusable “game board” that can be folded up and stored between uses. Use the cloth on grass, carpeting, or other surfaces where it is less likely to slip underfoot. Beanbags aren’t required, but the “marking stone” needs to be something that won’t roll away when tossed—or blow away if used outdoors.

If the weather isn’t cooperating for outdoor activities, or if you don’t have a suitable surface for chalk, or even if your students are just not excited about going outside and jumping around where anyone in the neighborhood might see them, these activities can also be done indoors by using masking tape or sticky-notes on the floor. You can even draw the grids on a large sheet of paper and use coins or game pawns as markers.

Filed Under: Activity Ideas, Auditory Learning, Homeschool How-To's, Kinesthetic Learning, Learning Outside the Books, Learning Styles, Math, Tactile Learning, Visual Learning, Workshop Wednesday

Workshop Wednesday: Sugar Cube Math, Part 2

May 16, 2012 by CarolynM 1 Comment

This topic has been explained in a previous post, but now we can supplement that with a photo. See the complete post HERE for detailed activities to make math understandable in such a fun way that it will prompt you and your kids to call it “SWEET!”

Notice that several activities are demonstrated in the picture: multiplication (upper left), showing that 2 rows of 3 cubes each is equal to 3 rows of 2 cubes each; volume (upper right), showing 3 layers of 3 rows with 3 cubes each, or 3x3x3; and the differences between area and perimeter (bottom). The four groups of sugar cubes at the bottom each contain 12 sugar cubes, so they all have an area of 12 units. However, the varying configurations show how the perimeter changes drastically. With the far right configuration, the sides in the middle hole could be counted as part of the perimeter, too, depending on the real-life application (e.g. if you were installing a fence along the sides of a trail, and the cubes represented the trail).

BONUS TIPS:
1) I wrote right on the cookie sheet with a dry erase marker and wiped it off with a tissue (but I did wash the pan well before putting it away).
2) The sugar cube activities can also be drawn on graph paper to save as a reference or worksheet.

Filed Under: Activity Ideas, Homeschool How-To's, Learning Outside the Books, Math, Tactile Learning, Workshop Wednesday

Workshop Wednesday: Building Blocks for Success in Math

April 18, 2012 by CarolynM 3 Comments

Math is called a foundational subject for good reason: if you don’t have a solid foundation, anything you try to build on top of it is in danger of falling apart. Math is also called a sequential subject, meaning that math skills must be mastered in sequence, each skill building on the skills before it. This picture represents my view of math skills and the order in which they should be mastered, starting at the bottom and building up, one skill upon another.

No one starts teaching math by instructing their preschoolers in differential calculus. The first math skill we teach is Sorting: Which ones match? Is this one like that one? We may start the sorting process with colors or shapes, but Sorting is still the basic skill being learned. Sorting is the #1 most important math skill, used from recognizing number value to solving the most complex equations. Counting is an extension of sorting, assigning a number name to each different quantity. We “know our numbers” when we can group the correct quantity of pieces to represent any given number. We have mastered counting when we can recite the quantities in ascending order. The ability to count backwards is preparation for further skills yet to come.

Place Value might be considered to be an extension of Sorting by placing 1-digit numbers together in one group, 2-digit numbers as another group, yet another with 3-digit numbers, 4-digits, and so on. Children who are learning to count past 10 are learning place value, even though they are not yet adding or subtracting large enough quantities to require carrying or borrowing. Those skills work hand-in-hand with addition and subtraction, but an understanding of place value has to come first. Using a large quantity of identical small manipulatives, such as toothpicks, you can demonstrate the quantities represented by numbers in the ones column and numbers in the tens column to show how and why we write numbers the way we do. As your student gains skill with addition, you can revisit Place Value to demonstrate carrying into the tens, hundreds, thousands, and as many columns as your child wishes to add.

The next natural step after Place Value is Addition. Your child may already be using his counting skills to inform you that since he already has 1 cookie, if you would just give him 2 more cookies, then he would have 3 cookies! He may not recognize 1+2=3 on paper, but he certainly understands cookie quantities! Addition facts are best learned through using real-life objects, manipulatives, or even diagrams, rather than just expecting a young mathematician to transfer immediately to written problems. Hands-on practice makes subtraction easily evident as the un-doing process for addition, thereby taking away the stigma that subtraction is yet another new skill to learn. If a student knows addition facts to the point of quick recall, that same student will be able to perform subtraction. Therefore, a student who struggles with subtraction is a student who has not mastered addition facts.

Multiplication is often presented as one more new skill to master, but when presented as a “short-cut” to repeated addition, the student will see multiplication facts as a convenient tool, not as an obstacle to further learning. Multiplication facts can be demonstrated with a large quantity of small manipulatives that can be grouped into repeated rows (½” squares of heavy paper or cardboard work very well). Some quantities of manipulatives can be rearranged to show various factors which result in the same amount, such as 1×12, 2×6, 3×4, 4×3, 6×2, and 12×1. Grouping and regrouping the manipulatives will give your student a deeper understanding of multiplication facts as he sees the groups (visual), arranges them with his own fingers (tactile), and repeats the facts aloud (auditory). A kinesthetic learner will prefer standing or kneeling to do this activity, providing yet another sensory element.

Why isn’t Division listed in these Building Blocks? Simply because Division is un-doing Multiplication, just as Subtraction is the un-doing of Addition. The only tricky part to Division is that sometimes things don’t come out completely even, and we get “left-overs”—but every child who has tried to share 5 cookies with 3 friends understands that concept already. Division uses the quick recall skills for multiplication facts to regroup as evenly as possible, and the “left-overs” will be dealt with in more detail later on as these skills progress even further into the concepts called fractions and decimals. By the way, fractions, decimals, and percents are all “nicknames” for the same amounts—they are just different ways of looking at the same quantities, such as ½, .5, and 50%, and those all mean that you and I are sharing equal amounts of the same cookie!

The final Math Building Block to be mastered is Logic. Logic means making sense of things, so they come out right. Logic may come in the form of “If/Then” statements, such as the block in the picture shows: If all cats have 4 legs, and Fido has 4 legs, does that then mean that Fido must be a cat? Fido might be a cat, but we also know that other animals besides cats have 4 legs, so we cannot assume that Fido is a cat until we have more information. That is logic: using information to prove a point, but sometimes you realize that you don’t have enough information yet, and the point you prove could be wrong. Another use of logic is in balancing equations. A very simplified example is 7-2=5; if we add 2 to each side, we’ll see 7-2+2=5+2 or 7=7, a true statement. What we do to one side of an equation must also be done to the other side to keep it balanced, as if the equals sign was the pivot point on a balancing scale.

If your student is struggling with any of these building block skills, back up and practice the previous block’s skills until they are mastered. Recall of these facts should come as easily as a reflex action before the student is ready to move on successfully to the next building block. Don’t worry that other students may be moving ahead already—they may not be ready either, and their “progress” will soon result in more struggles. Remember that a student who cannot do division does not know multiplication facts well enough. A student who struggles with multiplication does not know addition facts well enough, and neither does the student who struggles with subtraction. A student who has trouble with addition does not understand place value or number values well enough. Success in math is achieved by mastering skills in sequence and building a solid foundation with each skill before attempting more challenging skills.

For more tips, see also:
Looking for the “Hard Part”
Why Does Math Class Take SO LONG?

Filed Under: Auditory Learning, Homeschool How-To's, Kinesthetic Learning, Learning Styles, Math, Roadblocks to Learning, Tactile Learning, Visual Learning, Workshop Wednesday

Workshop Wednesday: Sidewalk Art

April 4, 2012 by CarolynM 1 Comment

What better way to incorporate drawing lessons into a beautiful homeschooling day than with chalk on the sidewalk or driveway? We often took our favorite storybooks outside with a bucket of chalk (and maybe a folded towel for under the knees) and picked some simple illustrations to duplicate.

Our favorites included the Little Miss and Mister Men characters by Roger Hargreaves and all of the fanciful creations of Dr. Seuss. Actually, we discovered that you can turn nearly any smiley-faced character into a Seuss-ian delight by adding an outcropping of tall feathers to the top of its head, a long, long, long tail, and brightly colored fur in zig-zaggy stripes. Now that’s a great lesson in cartooning! Encourage your budding artists to make a game of adding more and more features to their creatures by calling out “Heads” or “Tails” and supplementing those traits. Give each character special talents or accessories, such as juggling ice cream cones, wearing a polka-dot necktie, or holding a dozen strings tied to gigantic balloons.

Be sure to take the time to admire each other’s masterpieces and praise their unique qualities. Give each artist a turn to tell about his or her drawing, pointing out details and describing techniques used, for informal practice at oral presentations. Most of all, have fun making silly drawings and enjoying the chalk antics.

Sometimes we made several individual drawings, and sometimes we connected multiple parts into a long scene that filled our front sidewalk for the full width of our property. One summer day when lots of neighbor kids were looking for something to break up the boredom, I drew a very basic chalk outline of an old-fashioned circus train that stretched out over several blocks of our sidewalk, assigning each block (one box car) to a different child. We discussed as a group what sort of things our train should have (planning and problem-solving skills), and the children chose what they wanted to draw (delegating skills). One drew a box car with two giraffes sticking their long necks out the top. Another drew a lion in a cage, and another chose to draw the train’s steam engine with great puffs of smoke billowing out the smokestack. Our train had a few clowns, bright colored flags and pennants, and the words “Circus Train” on the side of yet another box car. The kids spent most of the afternoon drawing and coloring with the chalk and adding special touches. When anyone finished his own section, he would go help someone else, giving them all a great feeling of teamwork. The finished sidewalk “mural” received lots of admiration and compliments from neighbors and was the object of several photographs by parents. The kids all put so much work into their circus train, that we were all very glad that we had no rain for several days afterwards! However, rain was usually seen to be a magical eraser that tended to bring new inspiration for more drawings instead of disappointment that the previous masterpieces were gone.

Obviously, a variety of chalk colors makes drawing more delightful, but don’t underestimate the value of plain white chalk. Your art students will discover shading on their own, as they go over and over a section to make the color more intense, and having a limited palette of colors will make them more creative with using patterns. Be careful to use chalk marked “sidewalk chalk,” as others may not wash off as easily. I once bought a box of beautiful colored chalk at a garage sale, only to discover that the intense colors left permanent stains on the clothing we were wearing when we used it! The knees and elbows and sleeve cuffs had deep colors ground in from kneeling and leaning on the drawings, no matter how careful we had been. One more point: chalk is soft and gets used up quickly on rough surfaces, so buy in bulk! No one wants to stop in the middle of drawing an enormous stegosaurus, just because he ran out of chalk.

Whether your creations are large or small, simple or elaborate, you can enjoy a nice day outside with chalk, learning to copy drawings from books or making your own creations. Starting with simple line drawings from a favorite storybook will help beginning artists gain confidence, since they don’t have to rely on their imaginations for inspiration. After all, a large blank sidewalk can be rather intimidating! Making your drawings LARGE increases the number of details that can be added: a small face may not have room for much more than eyes and a smile, but a big face can also hold eyelashes, freckles, glasses, or a handlebar mustache!

Filed Under: Activity Ideas, Homeschool How-To's, Kinesthetic Learning, Learning Outside the Books, Tactile Learning, Visual Learning, Workshop Wednesday

Workshop Wednesday: Freebie Magnets

Workshop Wednesday: Clothespins

Workshop Wednesday: Building Blocks for Success in Spelling

Workshop Wednesday: Hopscotch – A Powerful Learning Game

Workshop Wednesday: Sugar Cube Math, Part 2

Workshop Wednesday: Building Blocks for Success in Math

Workshop Wednesday: Sidewalk Art

Now Available as eBooks!

Got Questions? Start Here!

Donate

Contact

Recent Comments

Monthly Archives

Categories